
Homeschooled First Grader (Braintree, MA)
Perimeter of a Circle
January 12 to 15- 2021
When I asked him, how he thought we could calculate the perimeter of a circle, he thought for a while and then asked me to draw two diameters in the circle with right angles with respect to each other.
Then he asked me to connect the points that these diameters touched the circle. Naturally, we got a square inside the circle. Then he told me that each side of the square is slightly smaller than the corresponding arch of the circle next to it. I asked him by how much. He responded it could be by one unit. I asked him how he know about it and why.
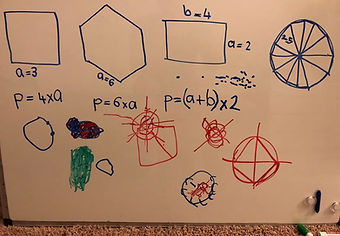.jpg)
He didn't have an answer. So, he changed tack. He tried to find a way to find the angle between the side of the square and the arch at the point that they touched. But it didn't get him anywhere too. So, he tried something new. He asked me to draw 4 more diameters in a way that we got a polygon with 12 sides. Then he told me that the sides of this shape are much closer to the size of the arch and hence they can be used to estimate the perimeter of the circle.
.jpg)
To drive my point home, we measured both diameters and perimeters of a couple of round objects using a measuring tape and wrote the values on the board. We then calculated the ratio of the two values. I eventually mentioned the concept of Pi. I also managed to find an excellent YouTube video about the history of Pi, which we watched.
One of the interesting points that we learned from this video was the fact that Archimedes was one of the first who tried to calculate Pi and his approach was very much similar to what Mortaza suggested: using polygons to estimate circles.