top of page

Homeschooled First Grader (Braintree, MA)
Geometry
Making a Dodecagon
October 28 - 2020 (1st grade)
One day, Mortaza told me that he had managed to build a polygon with 12 sides using his magnets. He told me that we could do it by adding a square to each side of a hexagon and then filling the gaps with equilateral triangles. Later we learnt that this polygon is called a dodecagon.

Pythagorean Theorem
October 30- 2020 (1st grade)
Mortaza found a set of round numbers that fits the Pythagorean Theorem. That is, 5, 12, and 13. In other words: 5^2 + 12^2 = 13^2
Drawing Polygons
November 16- 2020 (1st grade)
Mortaza learnt how to draw polygons using a compass and a protractor.
See his drawings here
2021
Perimeter of a Circle
January 12 to 15- 2021 (1st grade)
I tried to teach Mortaza the concept of the perimeter of shapes in geometry. Naturally, I started with simple shapes like squares and rectangles. He got the concept fairly easily. Then I asked him, how he thought we could calculate the perimeter of a circle. It then got interesting.
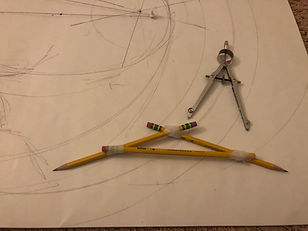
How to Draw Large Circles
January 20 - 2021 (1st grade)
I asked Mortaza how we can draw circles larger than what can be drawn with his compass. He instructed me to tape three pencils together as can be seen in the left image. He then mentioned that he had gotten the idea from one of the videos he had watched.
Then I showed him how we can draw even larger circles with a pin as the center and a piece of looped thread around the central pin and a pencil. Then we used two pins to draw ovals.

Perimeters and Areas of Shapes
January 29 - 2021 (1st grade)
We talked about the perimeter of other shapes. Mortaza wrote the equations for the perimeters of squares and rectangles. I asked him if he knows how to calculate the perimeter of triangles. He said there were different types of triangles. He then drew the shapes of these types and wrote the equation for the perimeter of each of them (Left). We also talked about the area of squares and rectangles. Then I gave him a problem to solve (below).
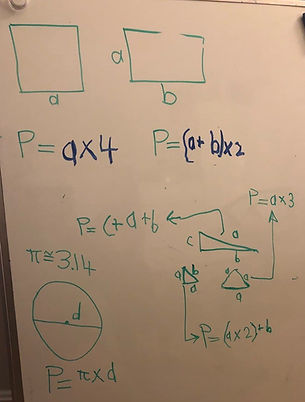.jpg)
.jpg)
Three Dimensional Star
May 11 - 2021 (1st grade)
Mortaza came to my room and told me that we wanted to build a three dimensional star. He then clarified that he wanted to build a 3D pentagram. In response to my question of how we could do it, he said "We build a dodecahedron and then attach the triangles to each face." The term dodecahedron sounded familiar but I couldn't remember what exactly it was. So, I looked it up. It is a solid with 12 faces which all faces are identical pentagons. Then I realized what he meant by "attaching triangles to each face". He meant we had to attach pentagonal pyramid to each face, and that was what we did. It seems that Mortaza came up with the idea of this shape by himself.
.jpg)
Since we didn't find a name for this solid, Mortaza gave it one: Harpes-hedron. later on, he found in a video that this shape had a name: stellated dodecahedron.
.jpg)
Mortaza first drew the shapes needed to build the dodecahedron and the pentagonal pyramids.
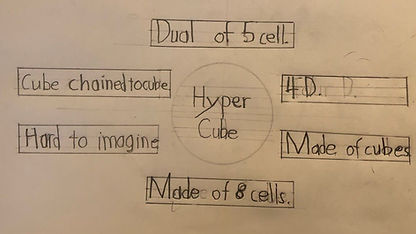
Show and Tell: Hypercube
May 19 - 2021 (1st grade)
Mortaza watched a series of videos about four dimensional solids and how they can be imaged in our three dimensional world. He then suggested that we build two different versions of hypercube as pale representations of four dimensional cubes. I helped him with building these hypercubes, but the ideas about the forms and shapes were purely Mortaza's. He also informed me that the hypercube is also called a tesseract. Mortaza then did a Show & Tell for his hypercubes. I asked him to first draw an idea-web to help him with his presentation.
.jpg)
.jpg)
.jpg)
Hyper-Tetrahedron
May 23 - 2021 (1st grade)
After building a hypercube, Mortaza suggested to build a hyper-tetrahedron, which is a four dimensional tetrahedron. Mortaza told me that it was also called a simplex. Of course, similar to hypercube, what we built was a pale representative of what we can imagine of a four dimensional shape. The solid consisted of one large tetrahedron, inside which were four smaller tetrahedrons; three at each corner and one in the center. Mortaza was very specific about how the center tetrahedron should be connected to the corner ones.
.jpg)
.jpg)

.jpg)
Building an Icosahedron
May 23 - 2021 (1st grade)
Mortaza's next solid was an icosahedron, which was a solid with 20 faces, each of which a triangle. Mortaza asked me to help him build this solid with paper. He said it was the dual of dodecahedron. That is, an icosahedron has 20 faces with 12 vertices, while a dodecahedron has 12 faces with 20 vertices. Later, we learnt about how we can find the dual of a solid. We just need to connect the center of each face to the centers of all adjacent faces. To help me understand what icosahedron looks like, Mortaza first built it with his magnets, and then flatten them to show me what pattern we should cut out a sheet of paper to build this solid. Then he used his protractor to draw the pattern on the paper. We then cut it out and glued it to make the solid.
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
.jpg)
Building a Truncated Octahedron
May 25 - 2021 (1st grade)
After icosahedron, Mortaza built a series of solids including this truncated octahedron.
.jpg)
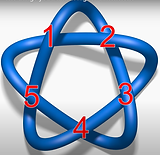
A knot with eight crossings
June 6 - 2021 (1st grade)
Mortaza watched a video in which there was a mention of knots with different number of crossings. It was clear to him that if we wanted a knot with an odd number of crossings (like 3 or 5 as shown in the top-right figures), we could use a star-shape with the same number of tips. However, he wanted to know how we can extend the idea to larger even numbers like 8. Here is the result of our attempt.
_bmp.png)
_bmp.png)
.jpg)
.jpg)
The sum of interior angles in polygons
May 29 - 2021 (1st grade)
Mortaza asked me if I knew what the sum of all (interior) angles in a rhombus was. I returned the question to him. He said it was 360 degrees. He was eager to explain to me how he found this fact. He said that I had told him before that the sum of angles in a triangle was 180 degrees, and since a rhombus is basically made up of two triangles, then the sum of its angles should be 360 degrees. It was obvious that he was very proud of his discovery.
After a couple of hours, I decided to challenge him along this road. I asked him if he could calculate the sum of interior angles in different polygons like a square, a pentagon, a hexagon, and so on. His answers were very interesting.
He said that square was easy since it was a special form of a rhombus, so the sum of angles was 360 degree. He then continued that the case of hexagon was very easy too. The sum of angles was 6*120. He explained: "Since hexagon is one of the shapes that can tile the plane, each angle of a hexagon should be 120 due the fact that each corner in a hexagon-tiling is shared between three hexagons. Therefore, each angle is 360 divided by 3."
.jpg)
His answer for a pentagon surprised me even further. After miming and whispering to himself for a couple of minutes he said that each angle in a pentagon should be 108 degrees. In an answer to my quizzical look, he brought his magnets and while showing me with his magnets, he explained: "if you fit three pentagons next to each other, the gap that remains will be a golden triangle. We know that the tip of this triangle has an angle of 36 degrees. Therefore, the angle of each pentagon would be one third of (360-36), that is 108 degrees.
I had no idea what "golden triangle" was. So, it took me a couple of video-watching and some thinking to understand how he came up with 108 as the interior angle of a pentagon.
A few weeks after this encounter, Mortaza asked me to download a new chemistry app on his iPad. I told him I would do it if he could calculate the interior angles of decagon and dodecagon (polygons with 10 and 12 sides respectively). To start the process I drew a dodecagon including the interior triangles. Then asked him what the angle of each triangle next to the center of the shape was. He correctly answered 30 degrees.
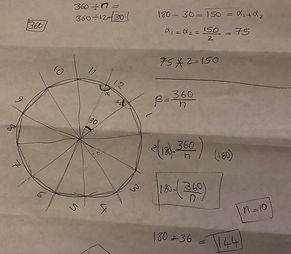.jpg)
He then continued that the other two angles were each 75 degrees and the interior angle of a dodecagon was 150 degrees. Before we continued to decagon, Mortaza was very eager to generalize his calculation. He then came up with this formula to calculate the interior angle of any polygon with n sides: 180-(360/n). We then calculated the interior angle of a decagon to be 144.
Speechless
June 16 - 2021 (1st grade)
I was getting out of the bed when Mortaza came to my room and out of nowhere asked: "Dad do you know what we get if we slice a tesseract along its diagonal?" Naturally I was dumbstruck. He continued: "We can use a Pascal's Triangle to get the answer." Which just added to my confusion. "Of course you remember what a Pascal Triangle is!" He added. This forcefully reminded me of myself when I wanted to remind my students about a well-known fact. When I found my voice, I told him that I didn't know the answer. He then said: "two tetrahedron and one octahedron." You can imagine that I didn't have the faintest clue what the question meant, let alone the answer. So, I asked where he learned about this. He said through a YouTube video. After watching the video I understood what he meant which was a fascinating concept to me.
What a tesseract is made up of?
June 27 - 2021 (1st grade)
Mortaza and I were talking about different shapes in geometry. At some point, I told him that a square is made up of 4 sides and a cube is made up of 6 faces, it would be nice to know what a tesseract (4D cube) is made up of. Without any hesitation, he replied: "It is made up of 8 cubical cells". It took me a while to convince myself that his answer was correct.
Three Dimensional Angle
August 23 - 2021 (1st grade)
During the months of July and August we didn't study much. Occasionally we had a little bit of book reading. During this time he had been obsessively and exclusively watching chemistry related videos. I was looking for an opportunity to turn his attention and hopefully his interest to another subject for a change. The opportunity presented itself on this late August day. Mortaza was playing with the measuring tape. He connected the books on my desk to the door and I don't remember exactly what else. Here is an image of his strange handiwork. I asked him if it was possible to measure the angle that the measuring tape made with the door. He said he didn't know. So, I told him that we could measure the sides of the triangle that the measuring tape
.jpg)
made with the door and then we could use the (inverse of) SINE or COSINE functions on the calculator to find the angle. Then I showed him how to do it. Mortaza then repeated the same calculation for another triangular shape in the room and it seemed that he understood the concept.
It was then that he asked one of his unusual questions: "How can we define a three-dimensional angle?" I tried to explain to him that an angle is by definition a two-dimensional concept, "It measures how narrow or wide the area between two crossing lines is." Mortaza kept insisting that we could define a three-dimensional angle and repeatedly used the word "sphere." To which I insisted that he was mistakenly using sphere instead of circle. After wrestling with each other for some time, at last I realized what he meant. What he was trying to tell me was that we defined the size of a simple angle by the length of the arc in front of it in a unit circle. The same concept can be extended to three dimensions when we had three lines in the space that crossed each other at the same point. Then the three-dimensional angle between these three lines could be defined as a measure of how thin or thick the pyramid shape between them was. What Mortaza was trying to tell me was that the size of this three-dimensional angle would be the same as the area of the portion of a unit sphere that faced this pyramid with the pyramid's apex at the center of the sphere.
To check if he really meant what I thought he meant, I asked him, "Imagine the whole unit sphere is 360 degrees, then what would be the 3D angle between the three lines that make the corner of the dresser?" He immediately answered 45 degrees. It took me a couple of minutes to convince myself that he gave the right answer.
Then he suggested, "Let's calculate the 3D interior angle of a regular tetrahedron."
I started thinking about how I could approach the problem. In the meantime Mortaza started playing with his triangular magnets. After a few minutes he said, it should be a little bit less than 18 degrees.
At first, I thought he was just guessing, but then I asked him how he knew this. He explained that each face of an icosahedron (a solid with 20 faces) is an equilateral triangle. Then if we connected the center of this solid to all its vertices, we would have had 20 tetrahedrons, but they wouldn't be regular tetrahedrons. I asked him how he knew this. He said that he had tried to make an icosahedron with his equilateral triangle magnets, but it wasn't possible. If this had been possible, then the 3D angle of a regular tetrahedron would have been 18 degrees. That is, 360/20=18. But since 20 regular tetrahedron with a common vertex did not fill the space to make an icosahedron, therefore the internal 3D angle of each tetrahedron should be slightly smaller than 18 degrees. Here is what Mortaza made with his magnets to reach this conclusion.
.jpg)
I was still in the process of digesting this argument when Mortaza asked me "how about an octahedron? what would be the 3D angle of an octahedron?" Then without waiting for an answer, he started working with his magnets again. For a second time, just after a few minutes, he shouted "It is more than 36 degrees", then he said something about octahedron and tetrahedron which I didn't catch. It took me more than half an hour of thinking with intense concentration to realize what he had figured out in a matter of a few minutes.
When I told him that "more than 36 degrees" might be right, he responded, "Well, I told you so." He figured out that we can fill the space with six "half-octahedron" and eight tetrahedron. Therefore, if the internal 3D angle of each tetrahedron was 18 degrees, then the internal 3D angle of each octahedron would be (360-8*18)/6=36. Since the 3D angle of each tetrahedron is less than 18 degrees. Then the 3D angle of octahedron will be more than 36 degrees. Here is what Mortaza made with his magnets to reach this conclusion. I searched the Internet and found that this is almost half of a solid called "cuboctahedron".
.jpg)
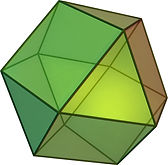
cuboctahedron
During the next couple of days, I couldn't help thinking about how accurate Mortaza's estimation of the 3D angle of a tetrahedron was. So, I tried to calculate the actual 3D angle through 2D integration of the part of the surface of a unit sphere that faced a tetrahedron internal angle. It was a lengthy and tedious calculation for me, but I managed to calculate the exact angle to be 16.22 degrees.
Three Dimensional Pythagorean Theorem
October 3 - 2021 (2nd grade)
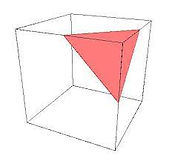
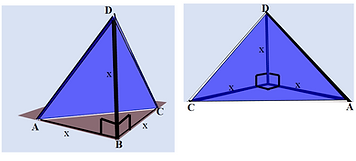
Mortaza came to me with the question of how we could have the Pythagorean theorem in 3D. He said let's consider a rectangular Pyramid in which all the lines at the apex of the prism made normal angles with each other. This could be the result of cutting out the corner of a cube with a plane.
His initial suggestion was that the 3D Pythagorean theorem could be stated as "The sum of the cube of the areas of the faces with a normal angle is equal to the cube of the area of the face in front of the normal angles." In his suggestion, each aspect in the regular Pythagorean theorem was upgraded by one level. That is;
-
2D --> 3D
-
length --> area
-
sum of square of two sides --> sum of cube of three faces
I was curious if we could verify it. It turned out when the sides next to the normal angles were all equal, then the math was not that difficult. We observed that his theorem was wrong but not entirely. For this special case, I proved "The sum of squares of the areas of the faces next to the normal angles is equal to the square of the area of the face in front of the normal angles."
I also made an Excel model that could do the calculation for the general case. It seems that the theorem for the squares of areas holds for the general case too. I searched the Internet to see if there was a similar interpretation of the 3D Pythagorean theorem, but I couldn't find one.
bottom of page
_bmp.png)
.jpg)